
“Why is it so difficult for my students to understand the notion of a limit? How can I help my students understand the derivative of a function?”
I have heard these questions so many times from Calculus teachers. Let’s face it, teaching Calculus to non-math students at college or university levels is hard! The “calculate this and that” approach students were used to in high school is not enough to make them successfully pass such a course.
Teaching students with a weak math background is ten times harder than those with a solid basis. But even with the latter, students find topics in Calculus often too abstract. If you are teaching Calculus online, these obstacles might become even more significant.
Considering this is a good starting point when designing your Calculus course and the learning objectives. Remember that not everyone enjoys math.
Take the time to evaluate a diverse range of learning materials. Deciding randomly right away on the first ones you see might cost you, later on, tons of extra teaching effort. Not to mention that your students’ comprehension efforts will suffer the most.
At the end of the day, you should aim for your students to be self-reliant when learning. Finding the most appropriate learning materials can help with that. Most traditional, and widely used, Calculus textbooks are designed for engineers and physics students, heavy on rigorous definitions, symbolic manipulation, and algebra skills. They often omit helpful conceptual explanations and present calculating procedures in a rote fashion, being more concerned with finding antiderivatives than understanding what the definite integral means.
Calculating procedures is useful but not more important than a strong conceptual basis. Among the calculus teachers that we have talked to, the majority express the thought:
By focusing on both the calculations and the conceptual aspects of Calculus, students understand the topics better, have greater success in their grades and are well equipped to apply their knowledge in further studies.

Ask yourself if the books and materials you select will meet your class’s needs and level. If you teach Calculus to life sciences or economics students, do you really need an epsilon delta definition of limits? These students might benefit from a less rigorous approach which is light in math syntax. In fact, the majority of students will.
In the US, for example, the number of students heading into the life sciences has more than tripled since 2000, and recent trends suggest that this dramatic growth is not slowing down. Something similar has happened to business and economics tracks. This makes us wonder if traditional Calculus courses, designed for a mathy audience, will meet the needs for the future.
A biology student may argue “But why is all this relevant for me.” Even if you explain its relevance, they might still feel the same about a subject they don’t like or understand.
Math teacher and author Ben Orlin recently published his book “Change is the Only Constant” where he addresses Calculus’ main topics with humor and a playful tone. His motivation for the book was to demystify the common belief that Calculus is unpleasant, boring and difficult to understand. During an interview, his answer to the question “There have been calls about revamping high school mathematics curricula to teach statistics, for example, as opposed to algebra and calculus. What are your thoughts on that?” was:
The questions are fair. And they demand that we reawaken our sense of the beauty and power of calculus. I think the different subjects accomplish different things. The kind of thinking you do in a calculus course is different from the kind of thinking you do in a good statistics course. I definitely don’t like the idea of abolishing calculus. But I taught in the UK for a few years, where there are not separate courses for algebra and geometry and calculus and so on. It’s an integrated math curriculum. Most countries work that way. You could move more of the math education into other subjects that are currently users of mathematics, like physics. In the UK, at least, the university system tends to work this way. If you’re majoring in the sciences, you’ll have math courses taught by the scientists. You won’t go to the math department to take those courses.
There are three features that, according to (D. Bressoud et al., 2015), are relevant for students when learning Calculus: confidence in their math ability, enjoyment of math, and their intention to continue studying mathematics (linked to the relevance of math in their future studies and careers).
How to increase the ranking of these factors? Precisely with a well thought teaching practice and suitable learning materials. Here is where teachers’ decisions play a significant role.
When students start studying university-level Calculus, they need a lot of support and guidance from teachers and tutors. Understandable explanations, many examples, and ways to visualize or contextualize the concepts help students understand the content. Besides, learners need constant encouragement and motivation, plus feeling listened to when they have comments and questions.
The new Calculus course in Sowiso was designed with these things in mind and works like a digital interactive Calculus textbook. It is meant to be used by first and second-year college/university students in and outside of STEM. Our course is a helpful complement when teaching calculus online.
The course is modular, so depending on your curriculum design, as a teacher, you can decide on the chapters, sections, and materials you want to include and which ones you want to leave out.

It includes the basic standard topics in Calculus plus a couple of more foundational chapters, Logic and Sets. These two were added for introducing students to the intricacies of mathematical reasoning and argumentation.
The theory includes engaging visualizations and tons of examples to illustrate abstract concepts and mathematical results.

Besides having our open randomized exercises that our teachers already know and love, our new Calculus course includes many graphical exercises. These assignments let students practice and learn in a more playful way.
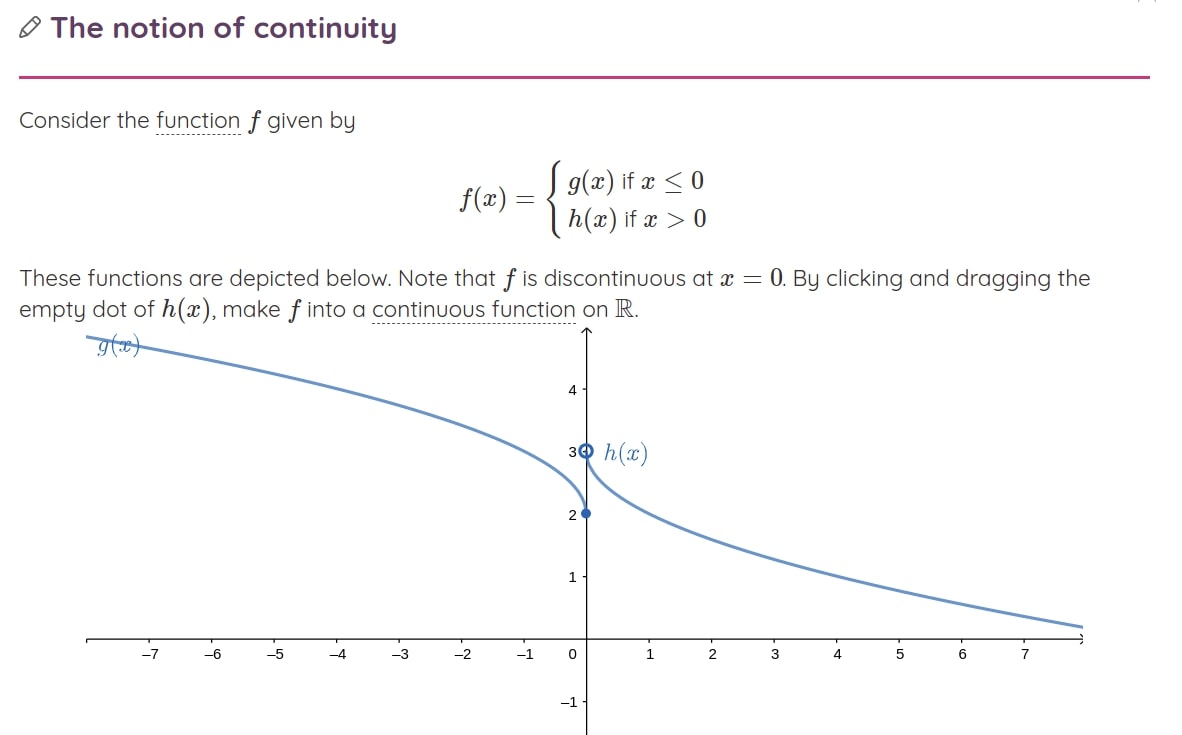
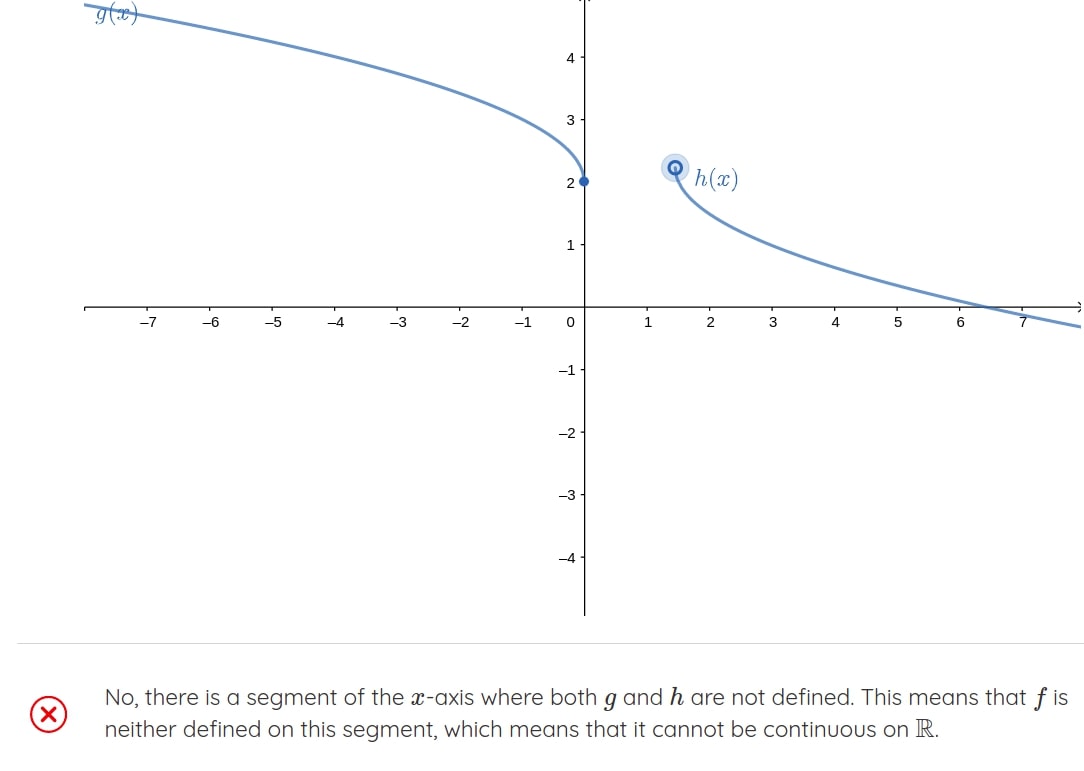
The graphical exercises also include on-point feedback for when students get stuck mimicking a personal math tutor.
Are you curious about our online Calculus course or generally exploring hybrid/flipped classroom approaches? Do you need help teaching Calculus online? Contact us at sales@sowiso.com! We can help you get started.

Dr. Michael McAssey of Amsterdam University College boosts student engagement through personalized courseware with automated feedback and grading.

Fully digital math courses helped Monash Universitys Anne Eastaugh to keep teaching even when lockdown protocols were enforced.

Learn how Dr Edna James of Algoma University was able to make her mathematics courses more accessible by integrating regular feedback and repeatable assessment in her classes.